計数値はばらつく
ガイガーカウンターなどの放射線量計は、γ線(光子)やβ線(電子)の数を一個一個数えます。この事を計数と言います。単位時間あたりの計数値(計数率)から放射線の強さが分かります。光子や電子は確率に従って飛び出すのですが、いつ飛び出すのかは決まっていないため、あまり短い時間だと正しい計数率が求められません。例えば、ガイガーカウンターなどでは、ピピッという音が1分間に100回鳴った場合に計数率100 cpm (counts/min)ということになりますが、最初の1分が100回であっても、次の1分は必ずしも100回にはなりません。これについて当研究室で行っている電子分光の例を挙げながら説明したいと思います。
飛び出す電子を数えて元素を特定する
当研究室では、表面を汚染した微量な元素を特定するために、オージェ電子分光法やX線光電子分光法を使用しています。オージェ電子分光法では電子を表面に入射して、X線光電子分光法ではX線を入射して、表面や不純物の元素から放出される電子の運動エネルギーと数を計測します。元素によって飛び出してくる電子のエネルギーが異なるので、ある元素特有のエネルギーを持った電子が観測されれば、その原子が表面に存在する事が分かります。オージェ電子分光法も光電子分光法も1原子層の1/100程度の量の元素を分析することが出来る大変感度の高い手法です。
オージェ電子分光の例
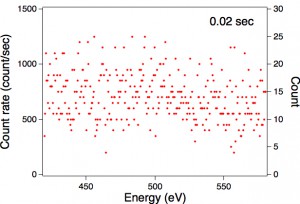
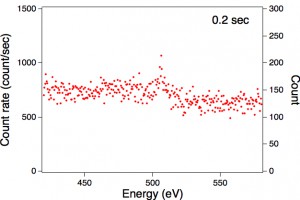
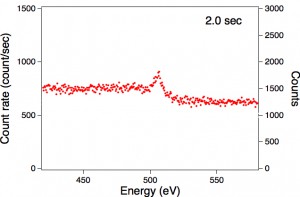
下のFig.1からFig.4は、ある結晶表面に水分子が数原子層程度吸着した同じ表面からのオージェ電子分光スペクトルです。横軸を電子のエネルギーにとり、縦軸(左側)を電子の計数率(カウント毎秒)にとり、各エネルギーごとの電子の計数率を赤い点で示したものです。Fig.1から4は、測定した時間の長さだけが異なっており、それぞれ0.02秒、0.2秒、2秒、10秒です。水分子の酸素からのオージェ電子は、エネルギー値500 eV付近にあるはずですが、Fig.1では計数率が上下にばらついていて全く観測できません。これは、各測定点の測定時間が0.02秒と非常に短いためで、実際の計数値(カウント)が10から20程度と小さいためです。計数値はそれぞれのグラフの右側の縦軸に示してあります。
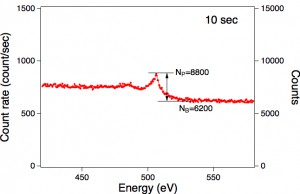
Fig.2,3,4と測定時間が長くなるほど、ばらつきが少なくなり505 eVにあるピークがはっきり見えてくることが分かると思います。これは時間が長くなったことにより、計数値が増えることが理由です。
独立な確率事象のばらつき
例えば、殆どの方はサイコロの1という目が1/6の確率で生じる事は知っていると思います。それでは、サイコロを6回振って1の目が出る確率を調べたらどうなるでしょうか?6回のうち、1の目が出る回数は0回のときもあれば1回や2回、また、それ以上のときもあります。6回のうち0回なら確率0、1回なら1/6、2回なら1/3、3回なら1/2になってしまい、本当の確率1/6からばらつきます。それでは6万回振ったらどうでしょう。この場合は(1の出た回数)/(6万回)は、かなり1/6に近づきます。
このような独立な確率事象の計数では、一般に計数値がN回のときその計数値のばらつき(誤差)が統計的に√N回程度になる事が知られています。つまり100カウントでは誤差が10カウントぐらいになり、計数値に対する誤差の割合は10/100=0.1程度になります。10,000カウントでは誤差100カウントになり誤差の割合は0.01です。したがって1%の精度で値を決めたい場合は、最低でも10,000カウントが必要ということになります。サイコロの例では6万回振れば1の目はおよそ1万回出るのですが、その場合の確率は1%の精度で決まることになります。
Fig.1からは計数が10ぐらいの時の精度が、Fig.2,3,4からはそれぞれ計数値が100,1000,7000ぐらいの時の精度を実感していただけるのではと思います。
バックグラウンドがある場合
さて、計数値の精度でもう一つ注意しなければならないのはバックグラウンドの問題です。Fig.4では酸素のピークは高いバックグラウンドの上に乗っています。この場合、本当に知りたいピークの高さは全計数の一部です。それに対して誤差はバックグラウンドも含めた全カウントNの平方根なので、ピークの高さに対する誤差の割合は相対的に大きくなります。また、バックグラウンドにも誤差がありますので、さらに誤差は増加します。
精度の良い計測のために
線量計で低レベルの放射線を計測するとき、計数率はせいぜい毎分数百回(数百 cpm)ぐらいです。100 cpmの場合、10%の精度で測定するためには最低1分の計測が必要になります。自然放射線によるバックグラウンド分を考えると、もっと長く測定する必要があるでしょう。線量計ではある一定時間の間の計数値から計数率を求めてシーベルト等に変換しています。この時間は時定数(time constant)と呼ばれて、機種によって違いますし、レンジによって切り替わる物もあります。精度の良い測定のためには、時定数を長くとって十分な計数値をカウントする事が必要です。時定数が長くできない場合は、何回も測定を行って平均をとる事で精度は向上します。
逆に、時定数と得られた計数率が分かれば、そのときの測定精度がだいたい分かります。例えば、時定数30秒で100cpmを計測したら、実際の計数値は50なので精度は√50/50=0.14、すなわち本当の値は100+-14 cpmの間にあると考えられます。10回測定して平均化すれば、計数値は500になるので精度は√500/500=0.045となり計数率の精度は約3倍高まります。

測定器には、様々な要因でどうしても固有の雑音(ノイズ)が存在します。周りにノイズの源がある場合もあります。ノイズは、欲しい信号に対してバックグラウンドとして加算されます。したがって、ある程度以下の低い信号レベルでは、相当長時間測定しても信号が見えて来ないことになります。その機器の測定限界です。
ガイガーカウンターの測定限界は0.1μSv/hぐらいです。そのレベルの測定値は、参考値程度と考えて値の上下に振り回されないようにしましょう。
ちなみにバックグラウンドも含むピークの強度が でバックグラウンドの強度が
でバックグラウンドの強度が の場合の誤差は、
の場合の誤差は、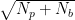 となります。
となります。
したがって真のピーク値 に対する誤差の割合は、
に対する誤差の割合は、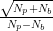 とバックグランドが高くなると大きくなります。
とバックグランドが高くなると大きくなります。
真のピーク値がバックグラウンドより大分小さい場合は、いくら長時間測定しても測定精度はなかなか上がりません。